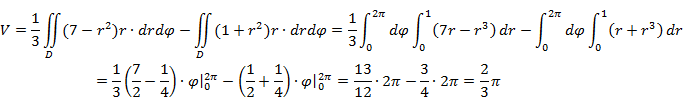3.Вычисление двойного интеграла в полярных координатах. Приложения двойного интеграла. Пример.

Вычисление двойного интеграла в полярных координатах:

Для вычисления двойного интеграла в полярных координатах применяют тоже правило сведения его к двукратному интегралу.

Если область ограничена лучами и , где и кривыми и , где , т.е. область правильная, то:

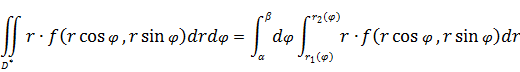
Пример:

Вычислить , где область – круг

Перейдем из декартовой системы координат в полярную:

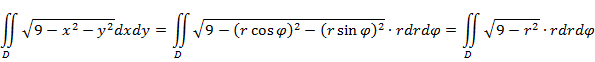
Область в полярной системе координат определяется неравенствами .

Область – круг, преобразовывается в область - прямоугольник. Поэтому:

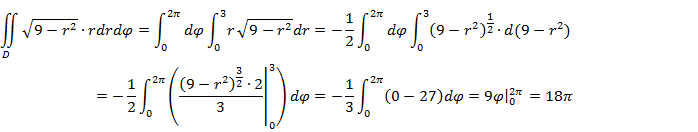
Приложения двойного интеграла:

1)Объем тела:

, где – уравнение поверхности, ограничивающей тело сверху.

2)Площадь плоской фигуры:

– в декартовой системе координат

– в полярной системе координат

3)Масса плоской фигуры:

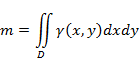
4)Статические моменты:

– относительно оси

– относительно оси

5)Момент инерции плоской фигуры

– относительно оси

– относительно оси

Пример:

Найти объем тела ограниченного, поверхностями и .

Данное тело ограничено двумя параболоидами.

Из системы находим линии пересечения: , .

Искомый объем равен разности объемов двух цилиндрических тел с одним основанием (круг ) и ограниченных сверху соответственно поверхностями и . Тогда:

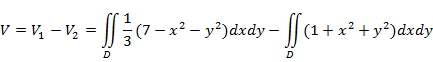
Перейдем к полярным координатам: