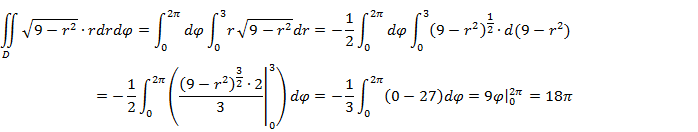2.Теорема о замене переменных в двойном интеграле. Пример.

Теорема:

Если функции и имеют в некоторой области плоскости непрерывные частные производные первого порядка и отличный от нуля определитель

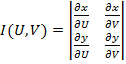, а функция непрерывна в области , то справедлива формула замены переменных в двойном интеграле: .

Частный случай – переход из декартовых координат в полярные. Тогда формула принимает следующий вид:, где - область в полярной системе координат, соответствующая области в декартовой системе координат.

Пример:

Вычислить , где область – круг

Перейдем из декартовой системы координат в полярную:

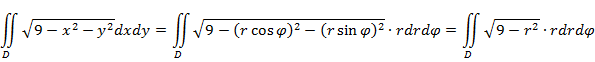
Область в полярной системе координат определяется неравенствами .

Область – круг, преобразовывается в область - прямоугольник. Поэтому: