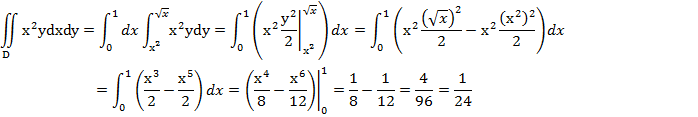1.Определение двойного интеграла. Теорема существования. Его свойства. Пример вычисления.

Определение:

Двойным интегралом от функции по ограниченной замкнутой области называется предел интегральной суммы, построенной для функции при неограниченном увеличении числа разбиений области на ячейки () и при стягивание каждой ячейки в точку (), если такой предел существует и не зависит от способа разбиения области на ячейки, ни от выбора в каждой из них.

Теорема существования:

Для всякой непрерывной функции в ограниченной замкнутой области существует двойной интеграл:

Свойства двойного интеграла:

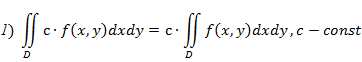
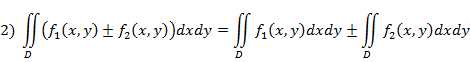
3) Если область разбить линией на две области и такие, что , а пересечение и состоит лишь из линии, их разделяющей, то :

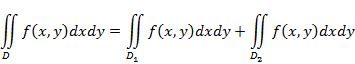
4) Если в области имеет место неравенство , то и . Если в области функции и удовлетворяют неравенству, то и

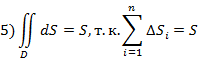
6) Если функция непрерывна в замкнутой области , площадь которой , то , где – соответственно наименьшее и наибольшее значения подынтегральной функции в области .

7) Если функция непрерывна в замкнутой области , площадь которой , то в этой области существует такая точка , что . Величину называют средним значением функции в области

Пример вычисления:

Вычислить в области , ограниченной кривыми и .