4.Определение функции нескольких переменных, дифференцируемой в точке. Определение полного дифференциала функции. Геометрический смысл частной производной.

Определение функции нескольких переменных, дифференцируемой в точке:

Функция называется дифференцируемой в точке , если её полное приращение в этой точке можно представить в виде , где и при и . Сумма называется главной частью приращения функции.

Определение полного дифференциала функции нескольких переменных:

Главная часть приращения функции , линейная относительно и , называется полным дифференциалом этой функции: .

Для независимых переменных и . Поэтому .

Геометрический смысл частной производной:

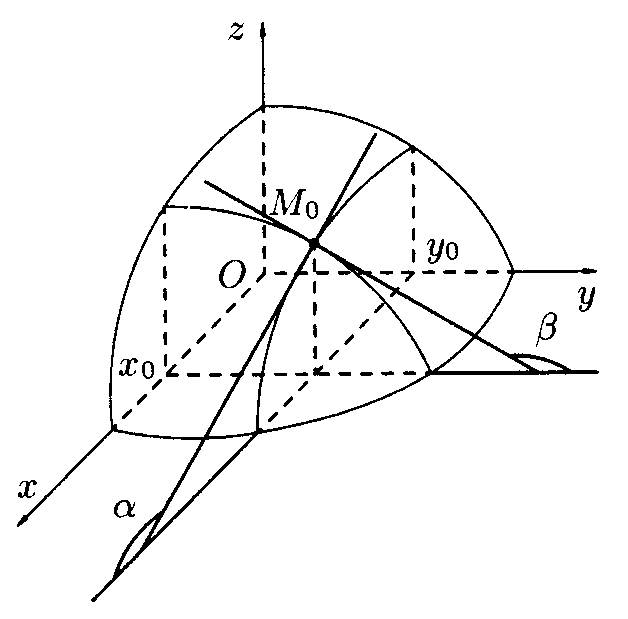Частная производная от функции в точке равна тангенсу гула, составленного осью и касательной к линии , проведенной в .