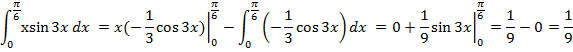13.Замена переменной и интегрирование по частям в определенном интеграле. Пример.

Теорема о замене переменной:

Если:

1)Функция и её производная непрерывна на

2)Множеством значений функции при является отрезок

3) и

То

Доказательство:

Пусть первообразная для на отрезке . Тогда по формуле Ньютона-Лейбница имеем Т.к. , то является первообразной для функции , . Поэтому по формуле Ньютона-Лейбница имеем

Пример:

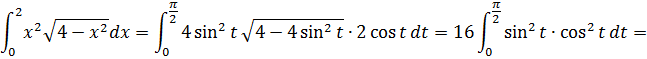
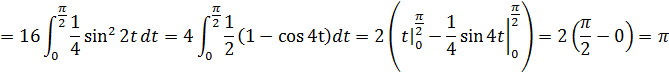
Интегрирование по частям:

Пример: