11.Теорема существования определенного интеграла. Его свойства

Теорема существования:

Для любой непрерывной на функции существует определенный интеграл.

Свойства определенных интегралов:

1.

2.

3.

4.Свойство линейности

5.Свойство аддитивности по области

6.Теорема о среднем значении функции:

Доказательство:

7.Теорема об оценке определенного интеграла

Доказательство:

Т.к. функция непрерывная на , то она достигает и , и очевидно, что находится между и

8.Если на , то .

Доказательство:

9.Если на то

Доказательство:

Рассмотрим на .

10.Производная от интеграла с переменным верхним пределом по переменному верхнему пределу равна значению подынтегральной функции, аргументом которой является переменный верхний предел.

Доказательство:

некоторая первообразная для функции

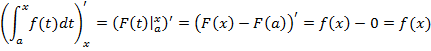
11.

Доказательство: