1.Определение производной функции в точке. Её физический и геометрический смысл.

Производной функции в точке называется предел отношения приращения функции к соответствующему приращению аргумента , при условие, что .()

Физический смысл производной:

Производная показывает скорость изменения функции в зависимости от изменения аргумента x.

Геометрический смысл производной:

Производная в точке равна угловому коэффициенту касательной к графику функции в точке, абсцисса которой равна .

2.Уравнение касательной и нормали к линии в точке. Пример.

Уравнение касательной:

.

Уравнение нормали:

(Т.к. нормаль перпендикулярна касательной, то её угловой коэффициент .)

Пример:

Найти уравнения нормали и касательной к функции в точке .

Решение:

- уравнение касательной

- уравнение нормали.

3.Необходимое условие дифференцируемости функции в точке.

Теорема:

Если функция дифференцируема в некоторой точке, то она непрерывна в этой точке.

Доказательство:

Пусть функция дифференцируема в некоторой точке x. Следовательно, существует её предел . Отсюда, по теореме о связи функции, её предела и бесконечно малой функции, следует: , где при , то есть . Переходя к пределу, при , получаем . А из этого следует, что функция непрерывна в некоторой точке x.

4.Теоремы о производной сложной и неявной функций. Примеры отыскания.

Теорема о производной сложной функции:

Если функция имеет производную в точке , а функция имеет производную в соответствующей точке , то сложная функция имеет производную в точке , которая находится по формуле .

Доказательство:

По условию . Отсюда, по теореме о связи функции, её предела и бесконечно малой функции, имеем или , где при .

Функция имеет производную в точке : , поэтому:, где при .

Подставив значение в равенство , получим: ; . Разделим полученное равенство на и перейдя к пределу при , получим .

Пример:

Найти производную .

Решение: .

Теорема о производной обратной функции:

Если функция строго монотонна на интервале и имеет неравную нулю производную в произвольной точке этого интервала, то обратная ей функция также имеет производную в соответствующей точке, определяемую равенством или .

Доказательство:

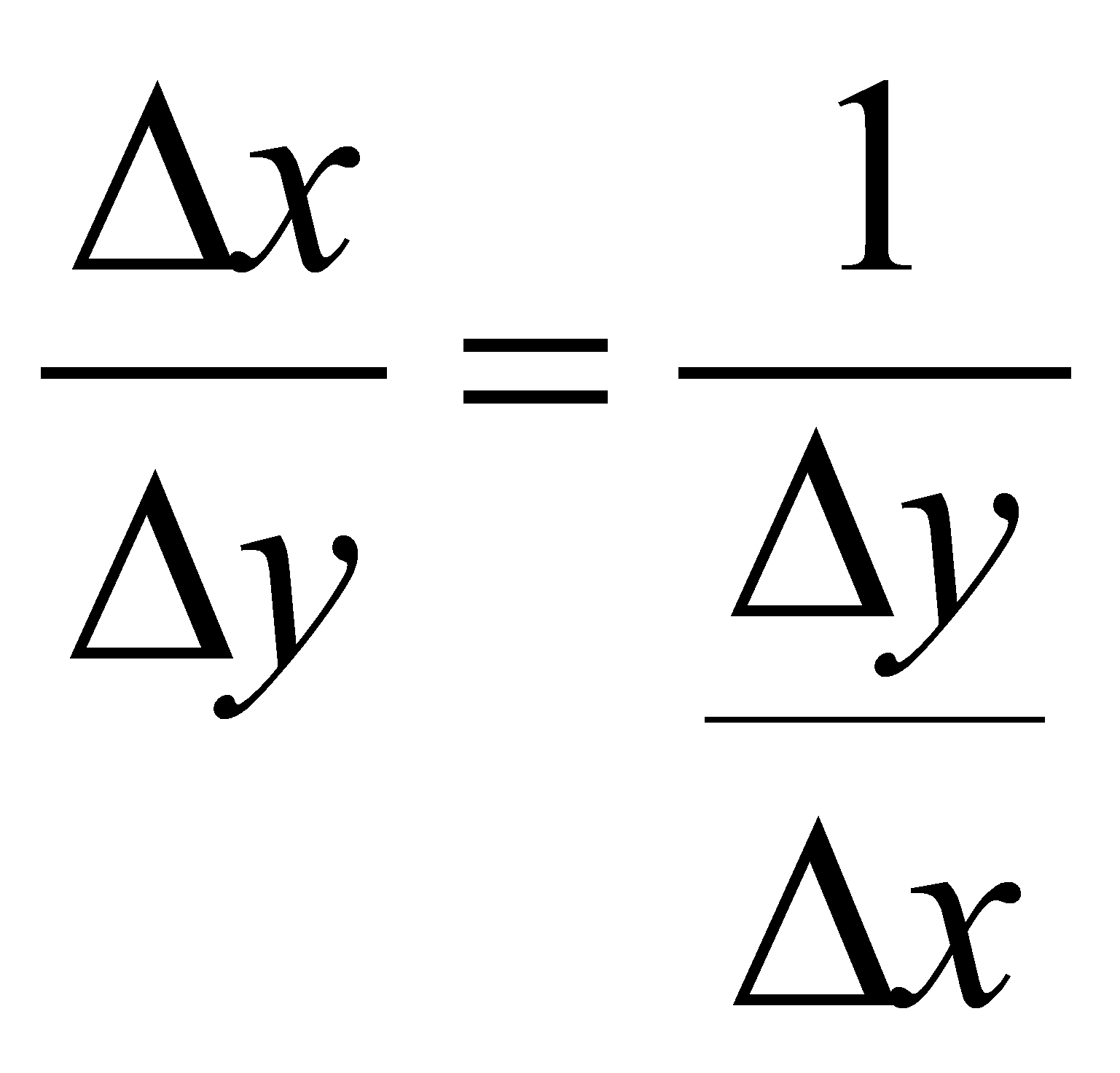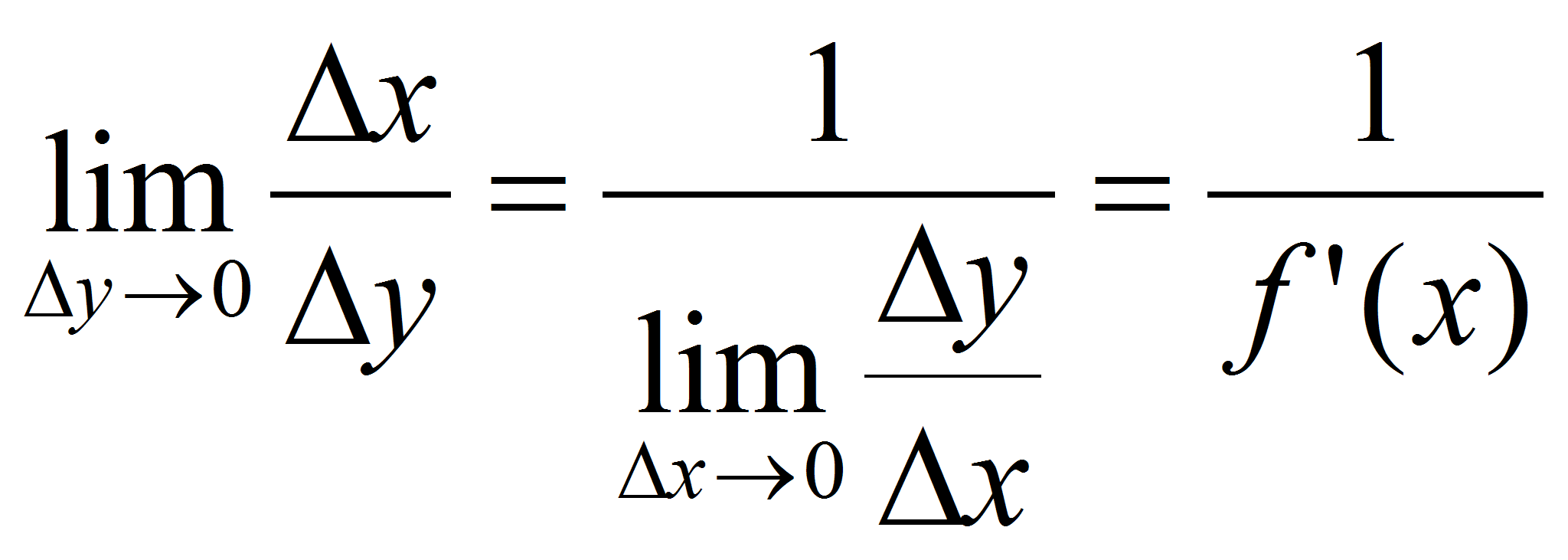Рассмотрим обратную функцию . Дадим аргументу приращение . Ему соответствует приращение обратной функции, причем в силу строгой монотонности функции. Поэтому можно записать: . Если , то, в силу непрерывности обратной функции, . И т.к. , то из следует равенство: , т.е. .

5.Таблица производных сложных функций.

6.Логарифмическое дифференцирование. Пример.

Найдем производную функции: .

Прологарифмируем обе части: .

Теперь найдем производную от обеих частей:

.

Пример:

Найти производную: .

Решение:

7.Дифференцирование неявных функций и функций, заданных параметрически.

Неявные функции:

Неявная функция- функция, заданная уравнением, неразрешимым относительно y.

Пример:

,

Решение:

Продифференцируем обе части: .

, .

Функции, заданные параметрически:

и - дифференцируемые.

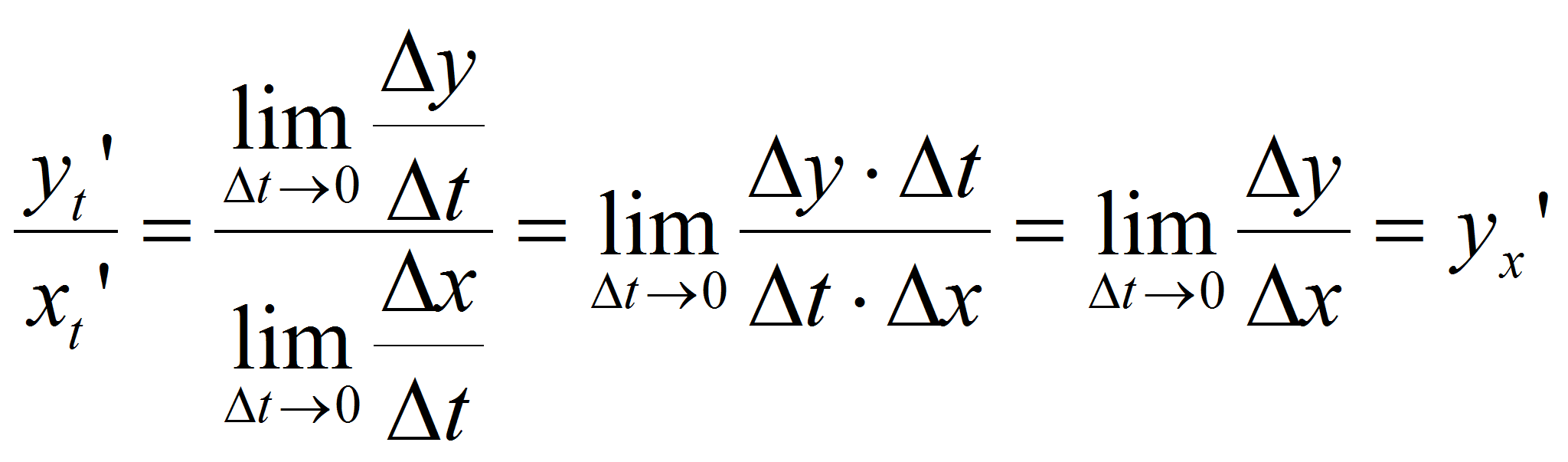, т.е.

Пример:

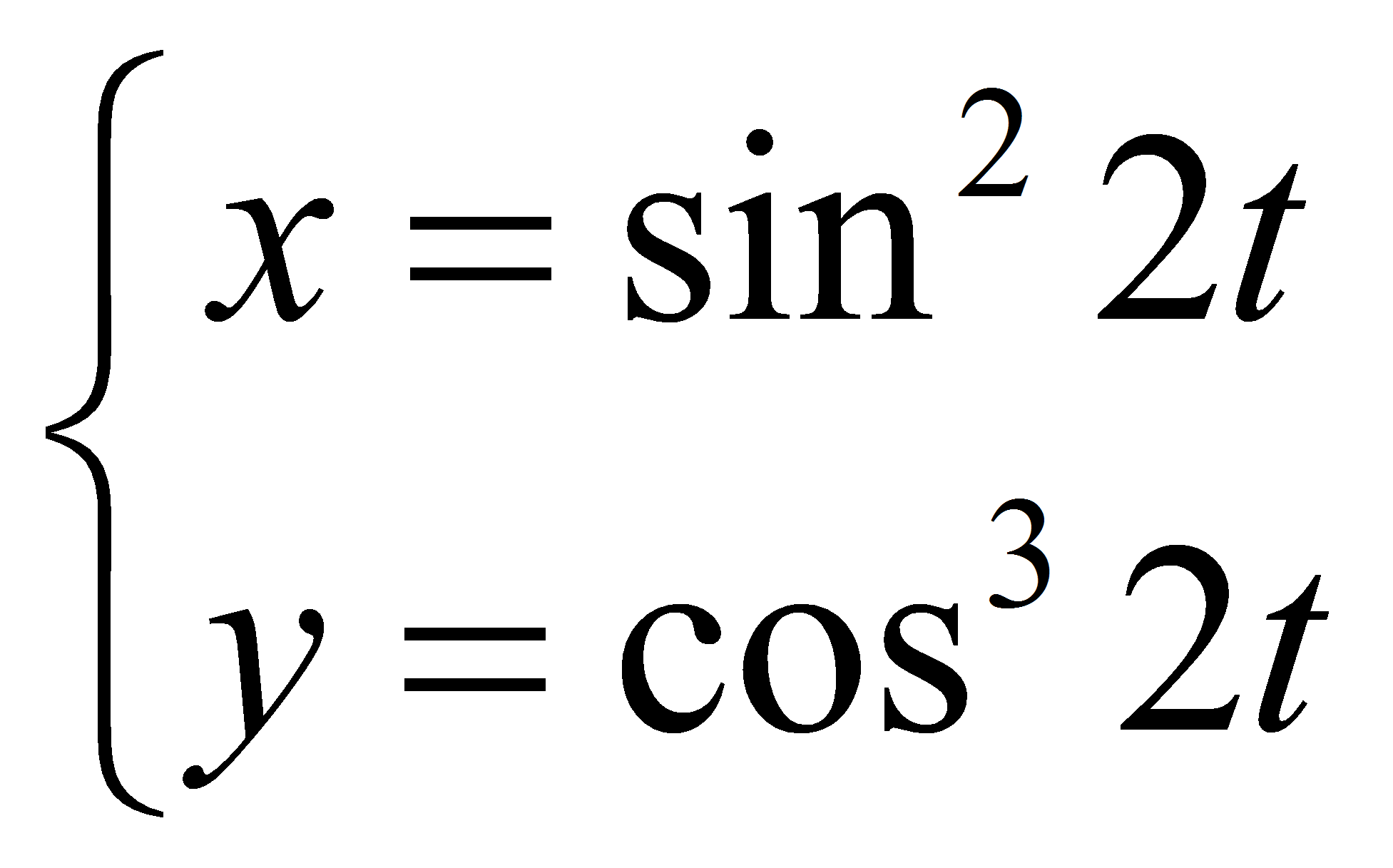
Решение:

8.Производные высших порядков функций, заданных явно, неявно, параметрически. Примеры.

1)Функции, заданные явно:

Производной n-го порядка функции называется производная от производной (n-1)-го порядка этой функции.

.

Пример:

Найти производную третьего порядка от функции:.

Решение:

2)Функции заданные неявно:

.

3)Функции, заданные параметрически.

.

.

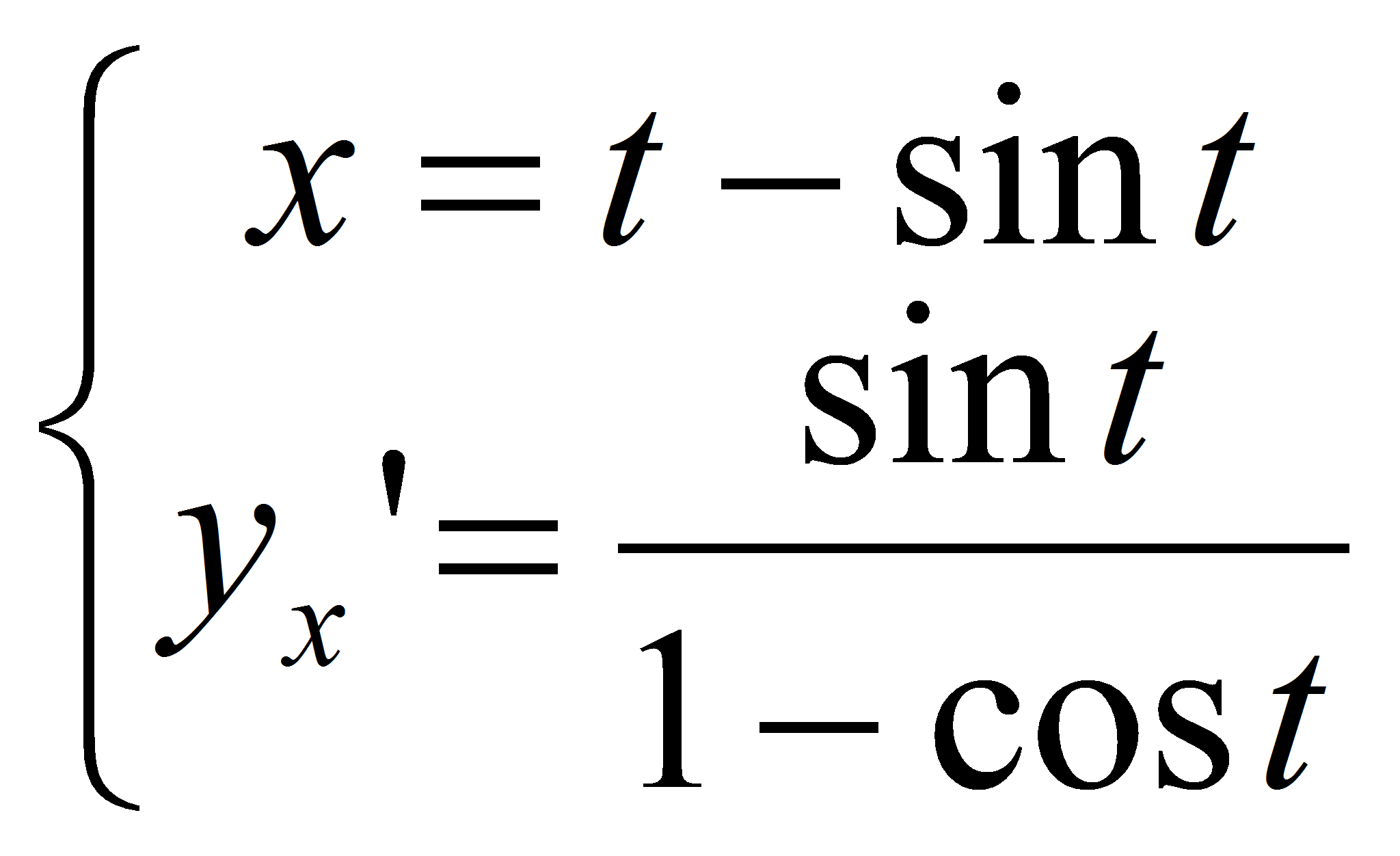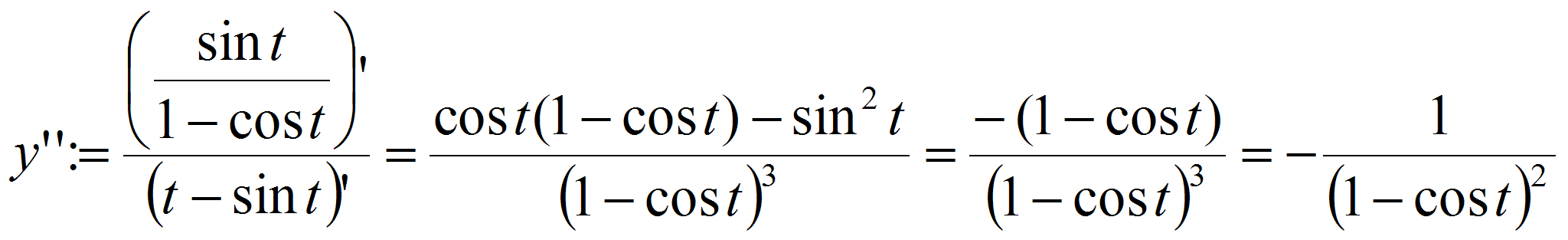
9.Понятие дифференциала функции, его геометрический смысл. Применение к приближенным вычислениям.

Дифференциалом функции в называется главная, линейная относительно , часть приращения функции.

.

Покажем, что и эквивалентные бесконечно малые при :

( - бесконечно малая).

Геометрический смысл дифференциала:

П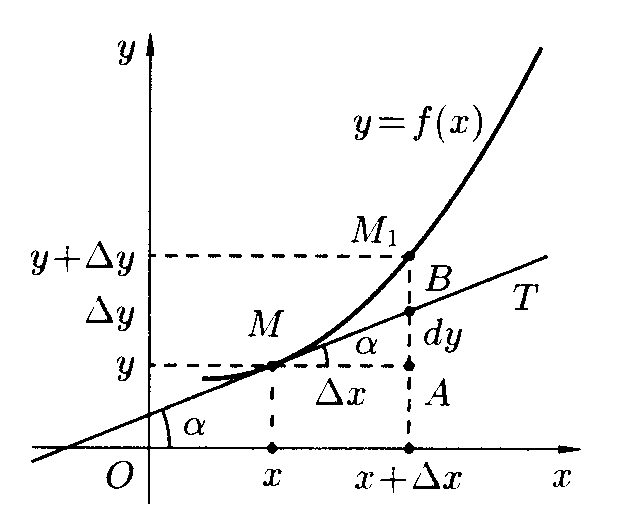роведем к графику функции в точку касательную и рассмотрим ординату этой касательной для точки . На рисунке , . Из прямоугольного треугольника имеем: , т.е. . Но, согласно геометрическому смыслу производной, . Поэтому или . Это означает, что дифференциал функции в равен приращению ординаты касательной к графику функции в этой точке, когда получает приращение .

Приближенные вычисления:

Пример:

Вычислить .

Решение:

, , .

.

10.Теоремы Ферма, Ролля, Лангража, Коши, Лопиталя о дифференцируемых функциях.

Теорема Ферма:

Пусть функция определена на и достигает своего наибольшего и наименьшего значения (M и m) в некоторой из . Если существует производная в , то она обязательно равна 0.

Доказательство:

Существует . Возможны два случая:

1), => , =>.

2), => , =>.

Из 1) и 2) следует, что

Теорема Ролля (о корнях производной):

Пусть функция непрерывна на и дифференцируема на и на концах отрезка принимает одинаковые значения: . Тогда существует хотя бы одна точка из , производная в которой .

Доказательство:

Непрерывная достигает на M и m. Тогда возможны два случая:

1), =>

2) наибольшее значение достигается внутри интервала по теореме Ферма.

Теорема Лангража (о конечных приращениях):

Пусть функция непрерывна на и дифференцируема на . Тогда существует хотя бы одна из , для которой выполняется следующее равенство: .

Доказательство:

Введем функцию . (непрерывная на и дифференцируемая на ).

,

Функция удовлетворяет Теореме Ролля существует , для которой: , ,,.

Теорема Коши:

Пусть функции и непрерывны на и дифференцируемы на , на . Тогда существует хотя бы одна внутренняя точка , для которой выполняется равенство .

Доказательство:

Введем функцию . (непрерывная на и дифференцируемая на ).

Функция удовлетворяет Теореме Ролля существует , для которой: , ,,.

Теорема Лопиталя:

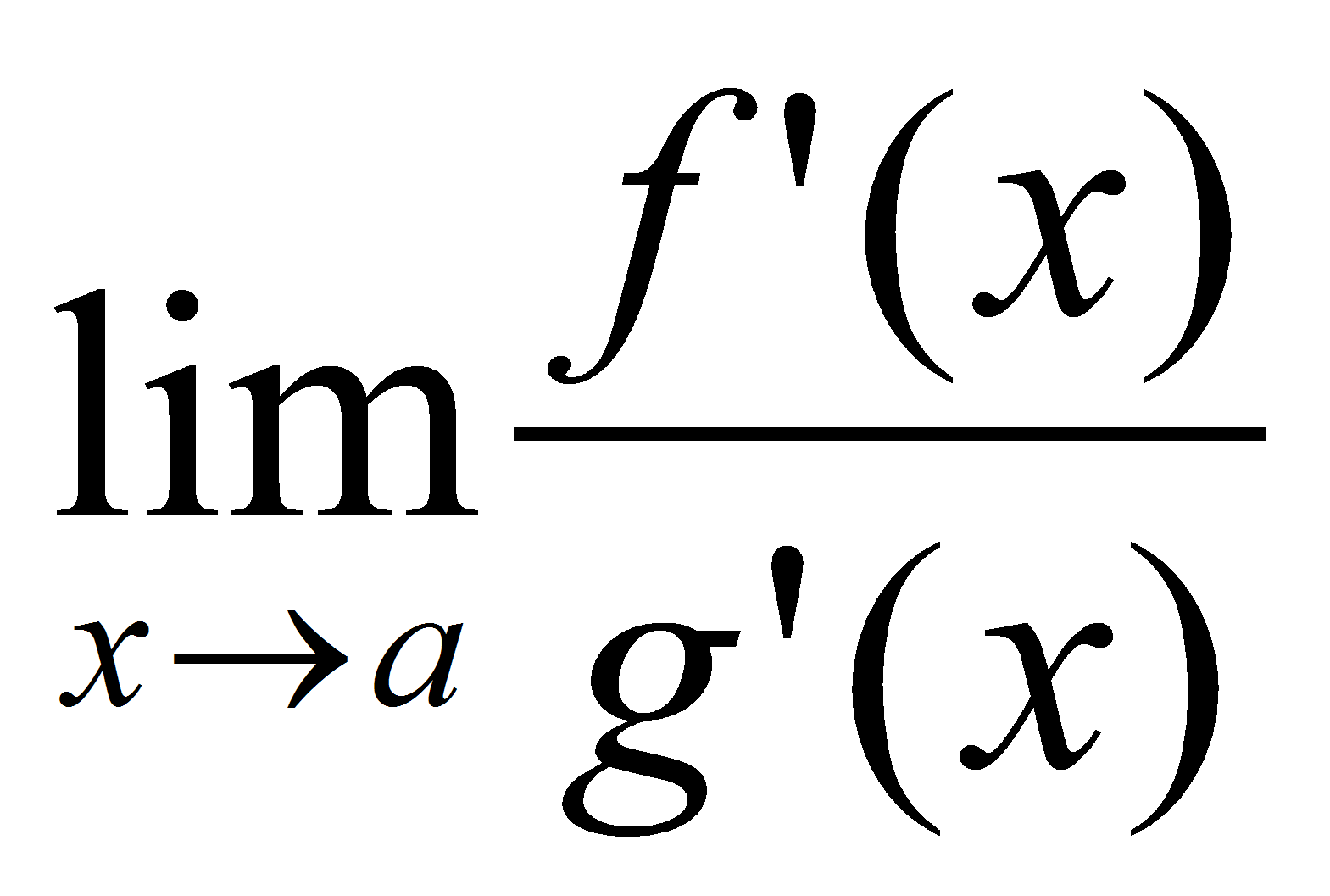Пусть функции и дифференцируемые в некоторой окрестности точки , , функции и либо бесконечно большие, либо бесконечно малые при и существует предел . Тогда существует предел .

Доказательство:

На отрезке применим и теорему Коши: .

Т.к. функции и бесконечно малые при , то ;

.
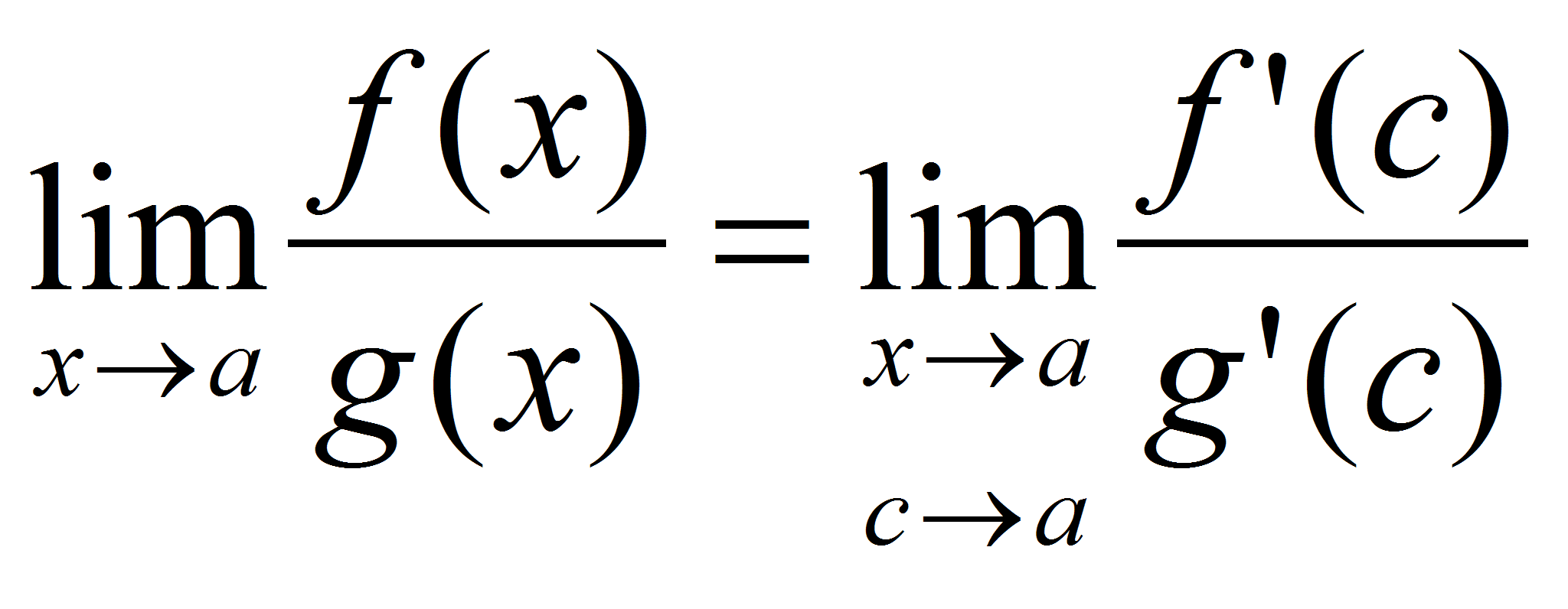