9.Понятие дифференциала функции, его геометрический смысл. Применение к приближенным вычислениям.

Дифференциалом функции в называется главная, линейная относительно , часть приращения функции.

.

Покажем, что и эквивалентные бесконечно малые при :

( - бесконечно малая).

Геометрический смысл дифференциала:

П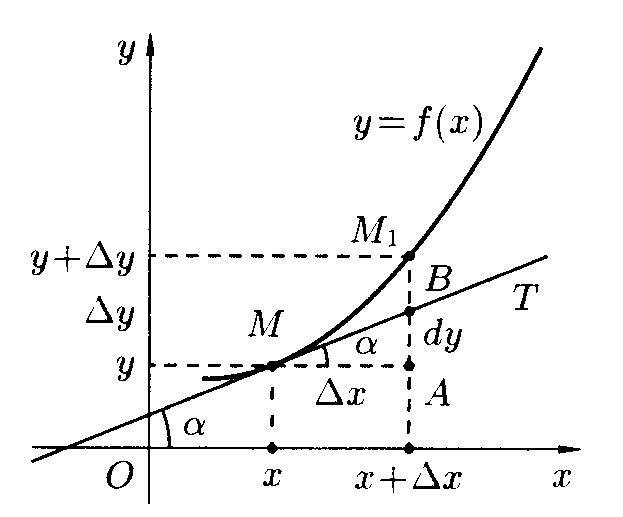роведем к графику функции в точку касательную и рассмотрим ординату этой касательной для точки . На рисунке , . Из прямоугольного треугольника имеем: , т.е. . Но, согласно геометрическому смыслу производной, . Поэтому или . Это означает, что дифференциал функции в равен приращению ординаты касательной к графику функции в этой точке, когда получает приращение .

Приближенные вычисления:

Пример:

Вычислить .

Решение:

, , .

.