4.Теоремы о производной сложной и неявной функций. Примеры отыскания.

Теорема о производной сложной функции:

Если функция имеет производную в точке , а функция имеет производную в соответствующей точке , то сложная функция имеет производную в точке , которая находится по формуле .

Доказательство:

По условию . Отсюда, по теореме о связи функции, её предела и бесконечно малой функции, имеем или , где при .

Функция имеет производную в точке : , поэтому:, где при .

Подставив значение в равенство , получим: ; . Разделим полученное равенство на и перейдя к пределу при , получим .

Пример:

Найти производную .

Решение: .

Теорема о производной обратной функции:

Если функция строго монотонна на интервале и имеет неравную нулю производную в произвольной точке этого интервала, то обратная ей функция также имеет производную в соответствующей точке, определяемую равенством или .

Доказательство:

Рассмотрим обратную функцию . Дадим аргументу приращение . Ему соответствует приращение обратной функции, причем в силу строгой монотонности функции. Поэтому можно записать: 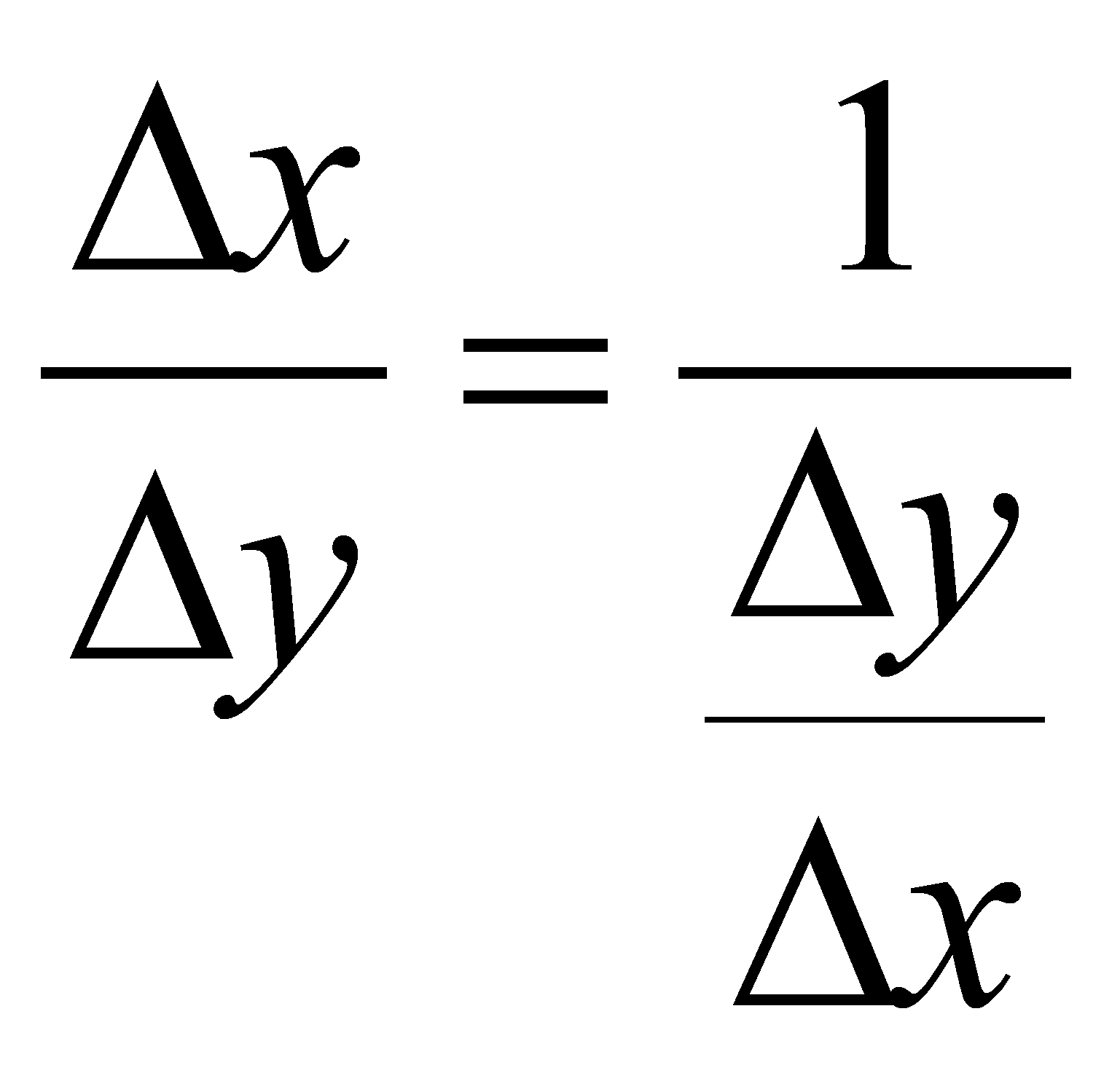. Если , то, в силу непрерывности обратной функции, . И т.к. , то из 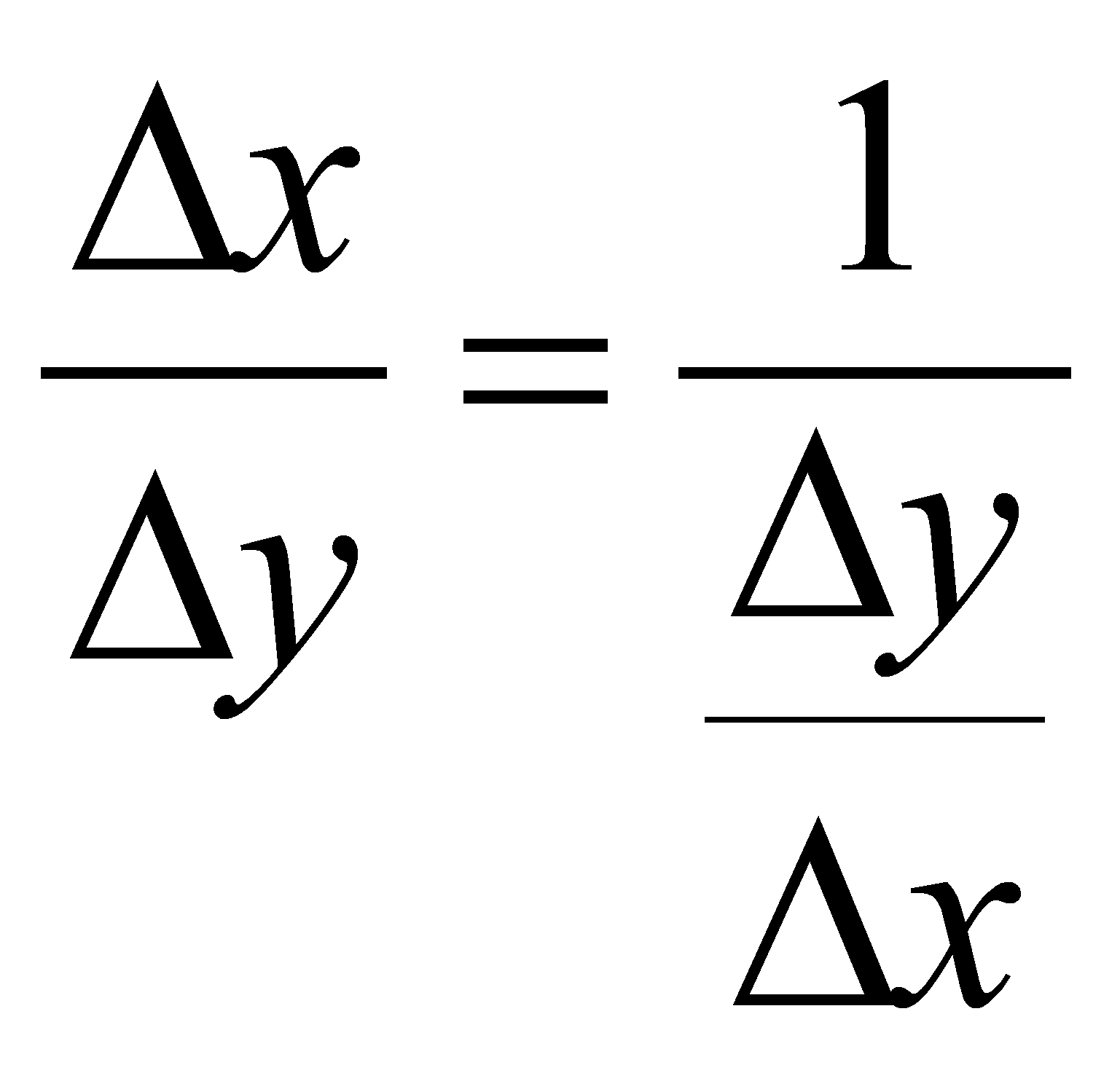следует равенство: 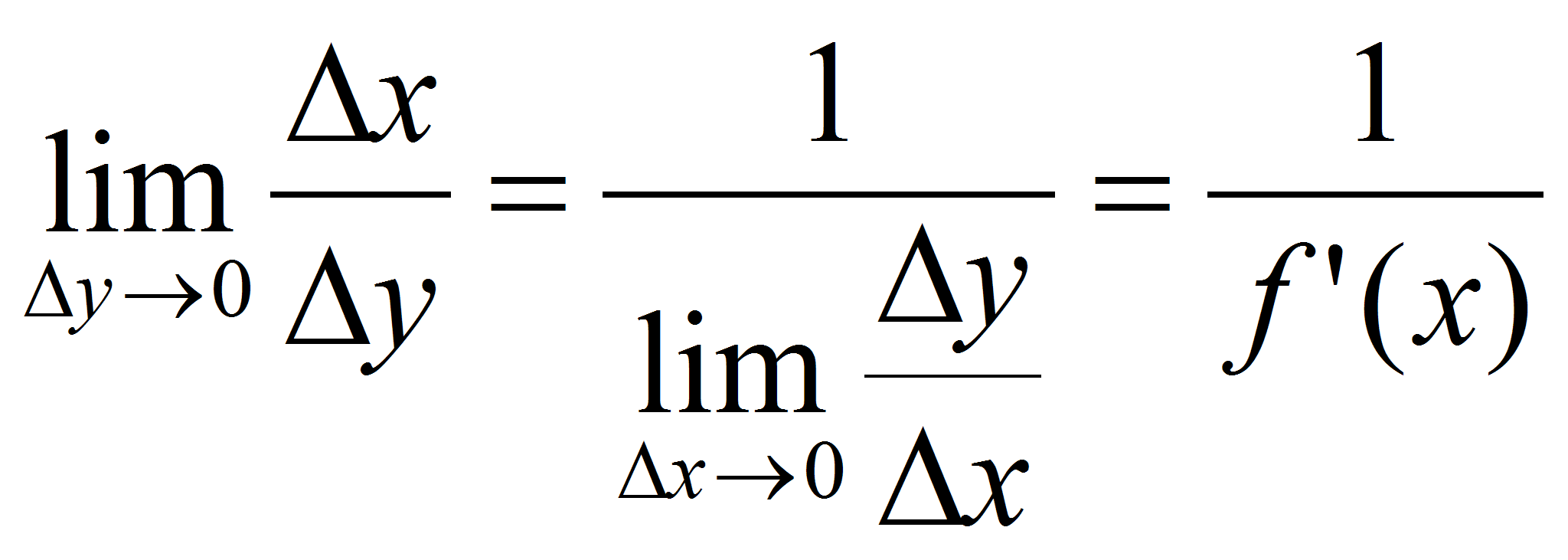, т.е. .