10.Теоремы Ферма, Ролля, Лангража, Коши, Лопиталя о дифференцируемых функциях.

Теорема Ферма:

Пусть функция определена на и достигает своего наибольшего и наименьшего значения (M и m) в некоторой из . Если существует производная в , то она обязательно равна 0.

Доказательство:

Существует . Возможны два случая:

1), => , =>.

2), => , =>.

Из 1) и 2) следует, что

Теорема Ролля (о корнях производной):

Пусть функция непрерывна на и дифференцируема на и на концах отрезка принимает одинаковые значения: . Тогда существует хотя бы одна точка из , производная в которой .

Доказательство:

Непрерывная достигает на M и m. Тогда возможны два случая:

1), =>

2) наибольшее значение достигается внутри интервала по теореме Ферма.

Теорема Лангража (о конечных приращениях):

Пусть функция непрерывна на и дифференцируема на . Тогда существует хотя бы одна из , для которой выполняется следующее равенство: .

Доказательство:

Введем функцию . (непрерывная на и дифференцируемая на ).

,

Функция удовлетворяет Теореме Ролля существует , для которой: , ,,.

Теорема Коши:

Пусть функции и непрерывны на и дифференцируемы на , на . Тогда существует хотя бы одна внутренняя точка , для которой выполняется равенство .

Доказательство:

Введем функцию . (непрерывная на и дифференцируемая на ).

Функция удовлетворяет Теореме Ролля существует , для которой: , ,,.

Теорема Лопиталя:

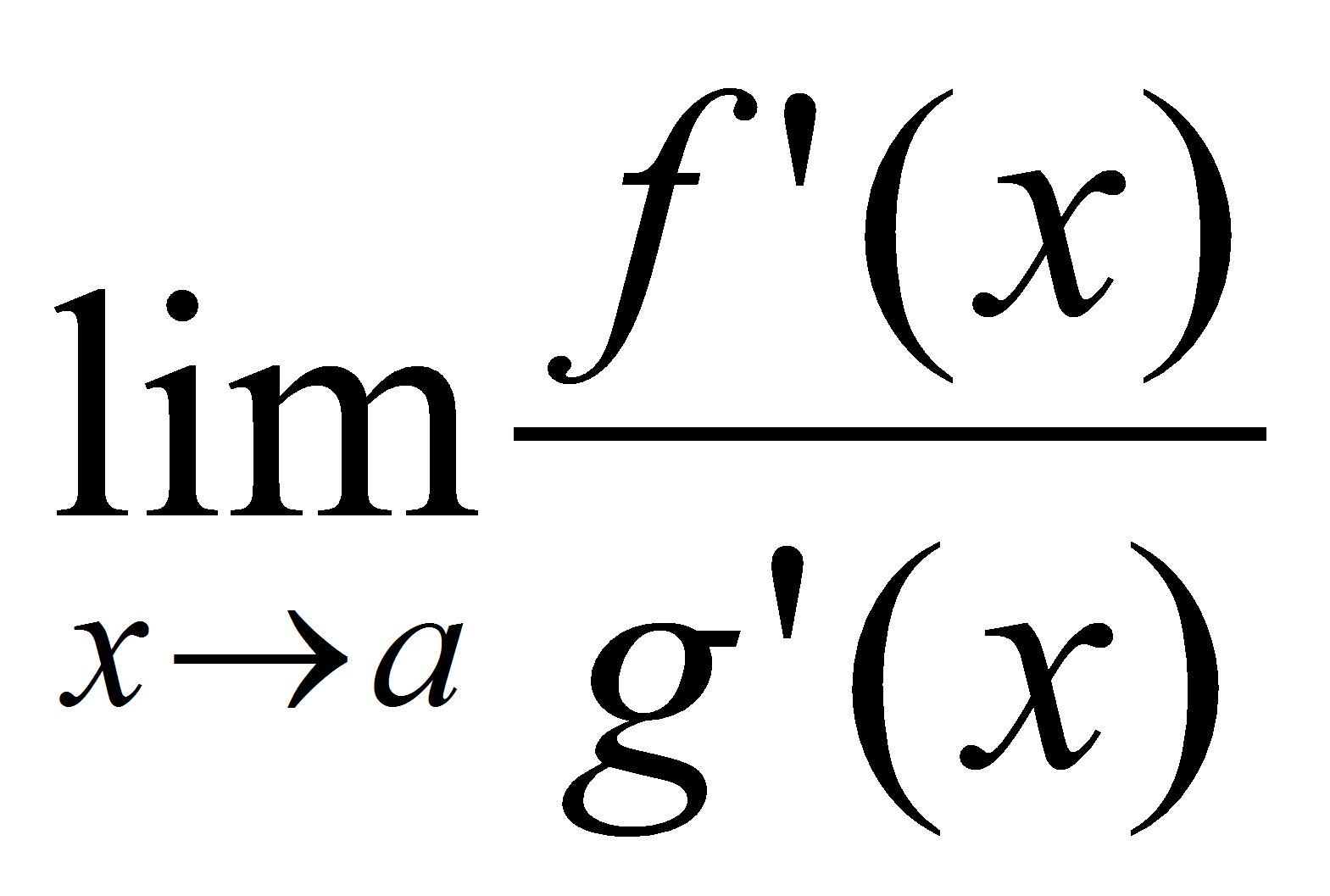Пусть функции и дифференцируемые в некоторой окрестности точки , , функции и либо бесконечно большие, либо бесконечно малые при и существует предел . Тогда существует предел .

Доказательство:

На отрезке применим и теорему Коши: .

Т.к. функции и бесконечно малые при , то ;

.
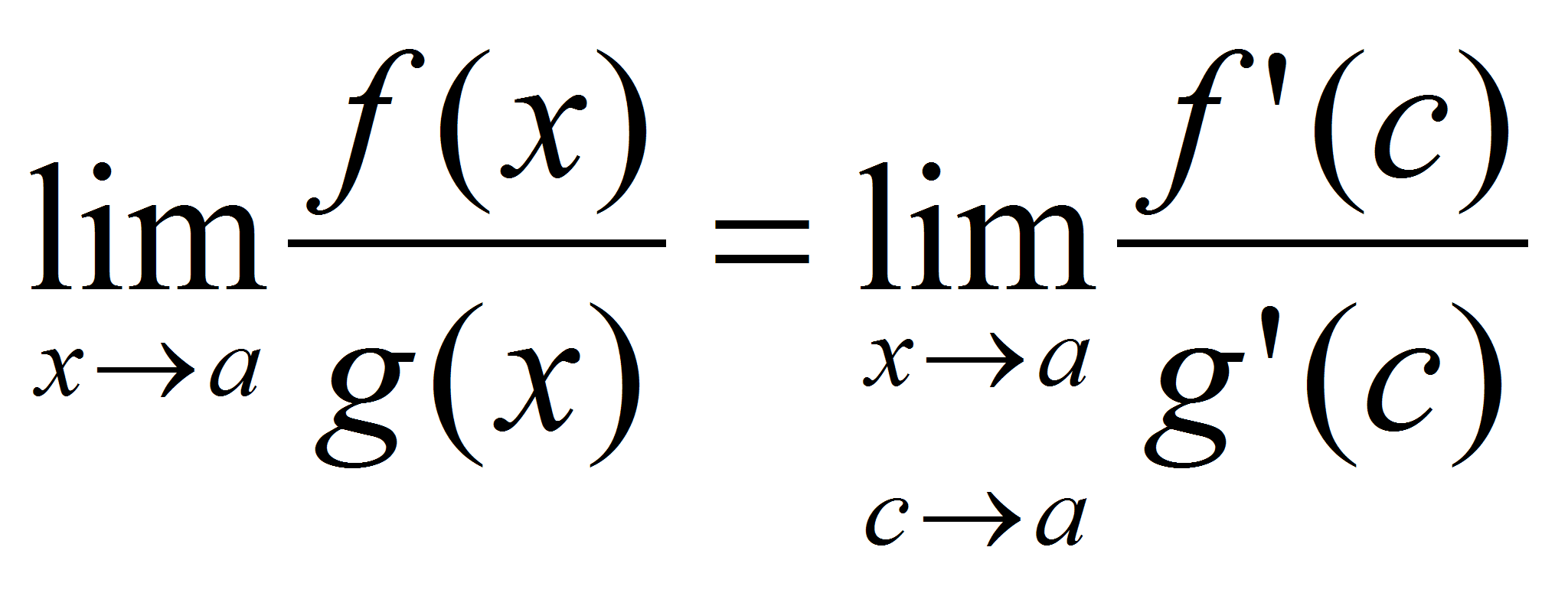