5.Теоремы о пределах суммы, произведения, частного двух функций. Первый и второй замечательные пределы. Примеры вычисления.

Теоремы:

1)Предел суммы двух функций равен сумме их пределов:.

Доказательство:

Пусть ,. Тогда по теореме о связи функции, её предела и бесконечно малой функции можно записать: и . Следовательно, , где - бесконечно малая функция (по свойству бесконечно малых функций). Тогда по теореме о связи функции, её предела и бесконечно малой функции можно записать , или .

2)Предел произведения двух функций равен произведению их пределов:.

Доказательство:

Пусть ,. Тогда и . Следовательно

,

.

Выражения в скобках, по свойствам бесконечно малых функций, - бесконечно малая функция. Тогда , т.е. .

2)Предел частного двух функций равен пределу делимого, деленного на предел делителя, если предел делителя не равен:.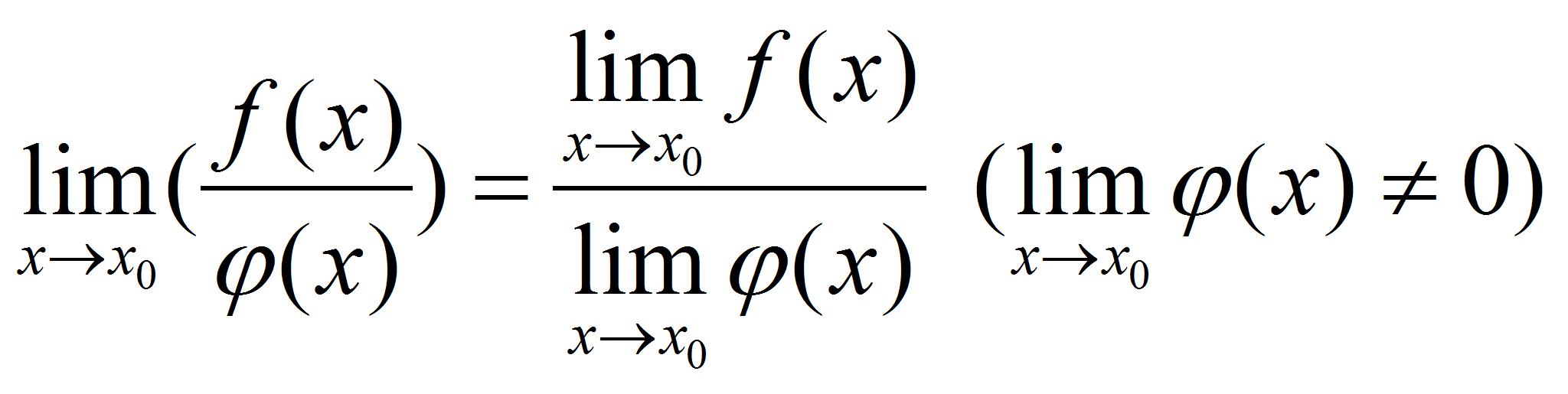

Доказательство:

Пусть ,. Тогда и . Тогда . По свойствам бесконечно малых функций, второе слагаемое – бесконечно малая функция.

Поэтому , т.е.

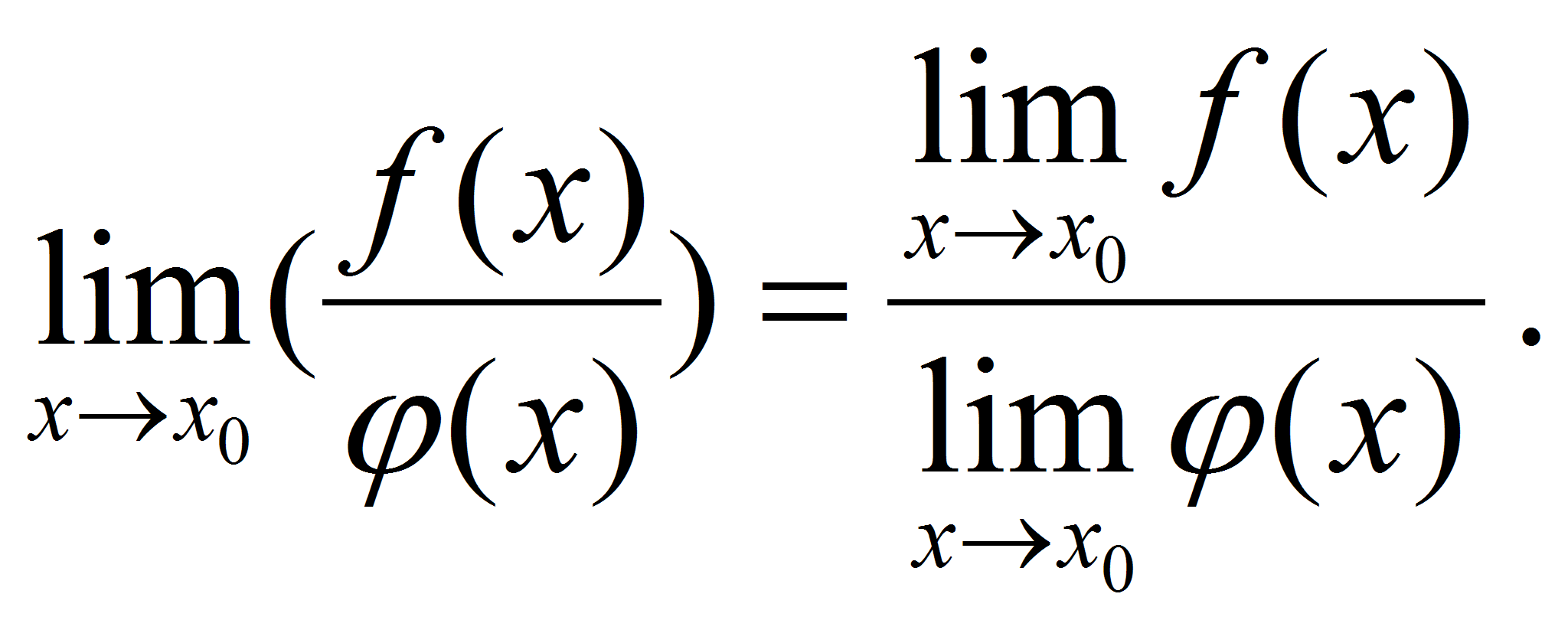
Первый и второй замечательные пределы:

1)Первый замечательный предел:

Пример вычисления:

.

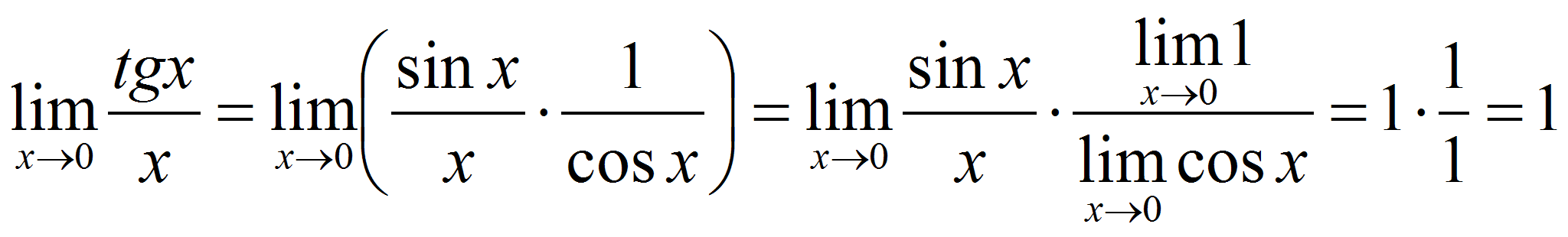2)Второй замечательный предел:

Пример вычисления:

Вычислим . Пусть . Тогда: .