зображенная
на рисунке функция
непрерывна на отрезке
и принимает свое наибольшее значение M
в точке
,
а наименьшее m
– в точке
.
Для любого
имеет справедливо неравенство:
.12.Свойства функций, непрерывных на отрезке: теорема Вейерштрасса, теорема о промежуточных значениях. Их геометрических смысл.
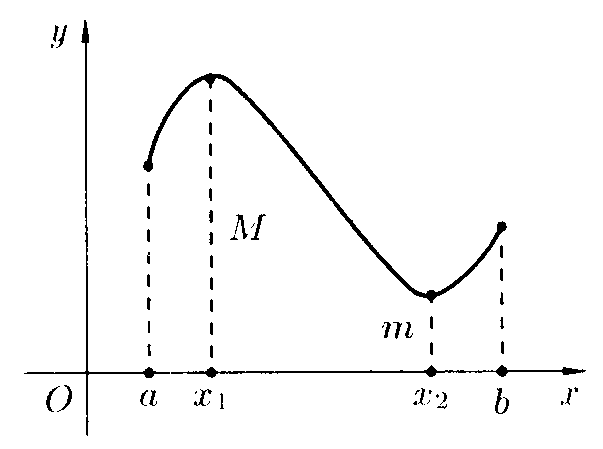
Теорема Вейерштрасса: Если функция непрерывна на отрезке, то она достигает на этом отрезке своего наибольшего и наименьшего значений.
Изображенная
на рисунке функция
непрерывна на отрезке
и принимает свое наибольшее значение M
в точке
,
а наименьшее m
– в точке.
Для любого
имеет справедливо неравенство:
.
Теорема о
промежуточных значениях: Если функция
непрерывна на отрезке
и принимает на его концах неравные значения
и
,
то на этом отрезке она принимает все промежуточные значения между A
и B.
Г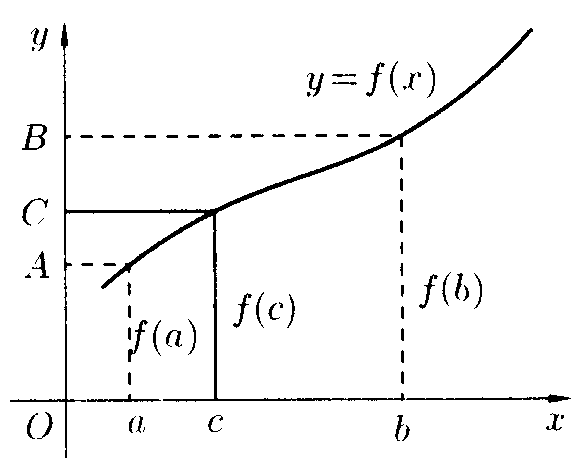
еометрически
теорема показана на рисунке.
Для
любого числа С, заключенного между A и B, найдется точка с внутри
этого отрезка такая, что
.
Прямая y=C пересечет график функции по крайней мере в одной точке.
