8.Определение квадратичной формы двух и трех переменных. Понятие матрицы квадратичной формы. Пример.

Квадратичной формой двух переменных называется однородный многочлен второй степени относительно этих переменных:.

Квадратичная форма трех переменных:

Матрица вида 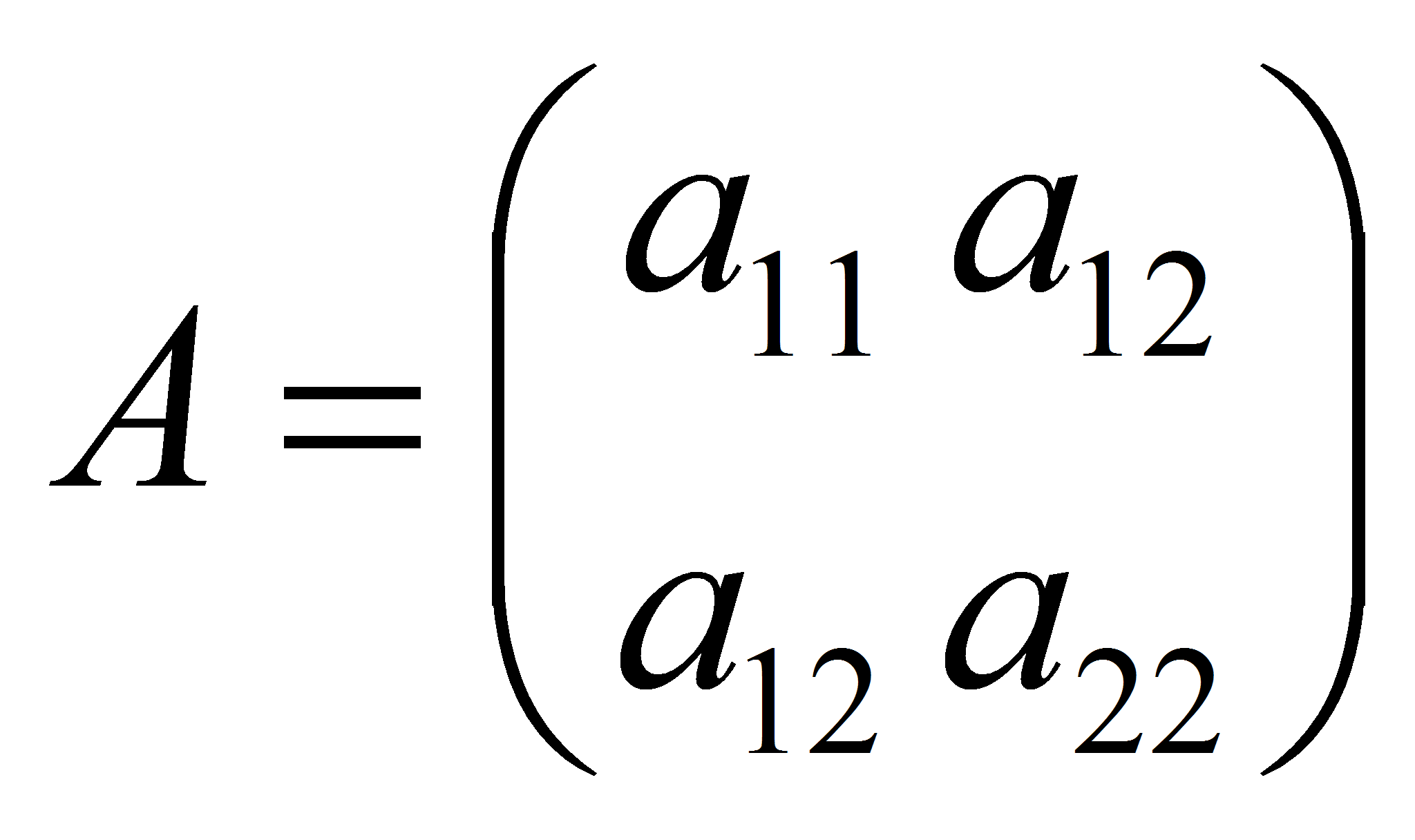называется матрицей квадратичной формы.

Квадратичная форма имеет канонический вид тогда и только тогда, когда её матрица имеет диагональный вид .

. .

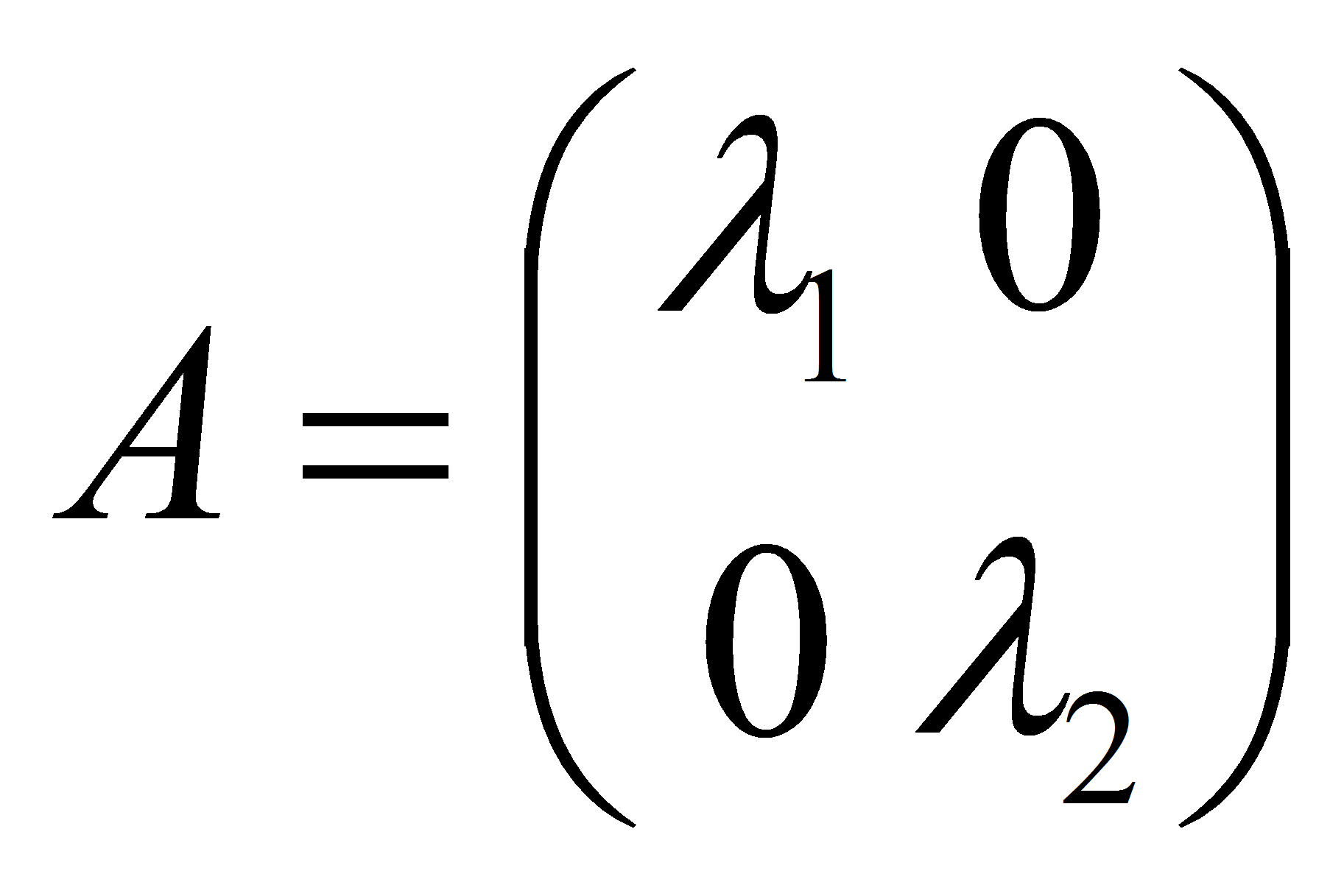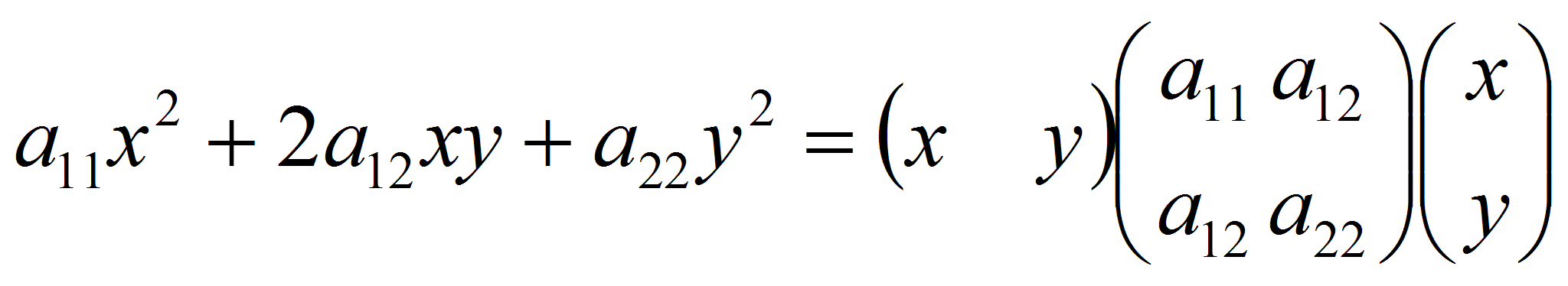Свойства квадратичной формы:

1)Матрица квадратичной формы симметрическая

2)Симметрическая матрица с вещественными элементами имеет вещественные собственные числа.

3)Собственные векторы, соответствующие различным вещественным собственным числам, ортогональны.

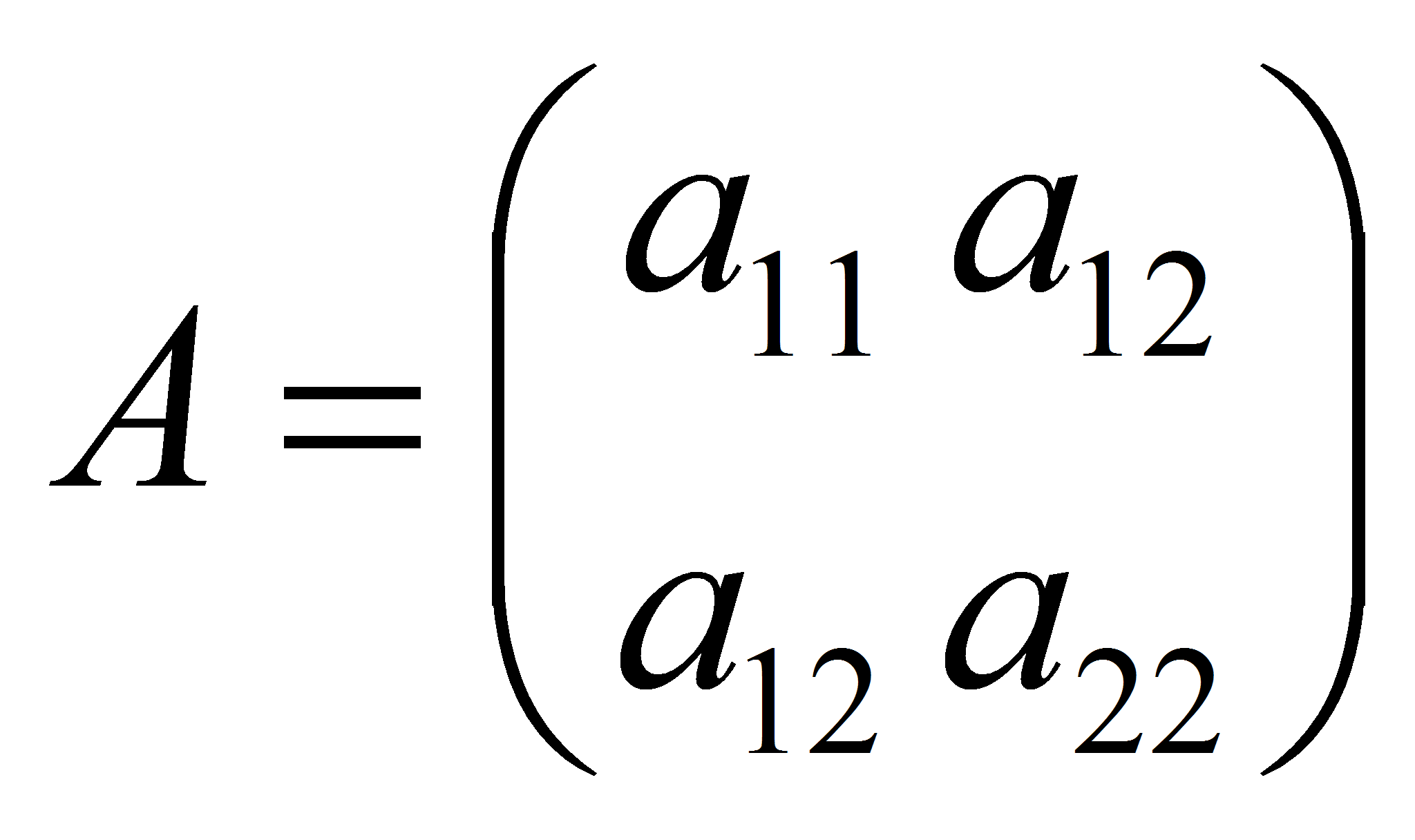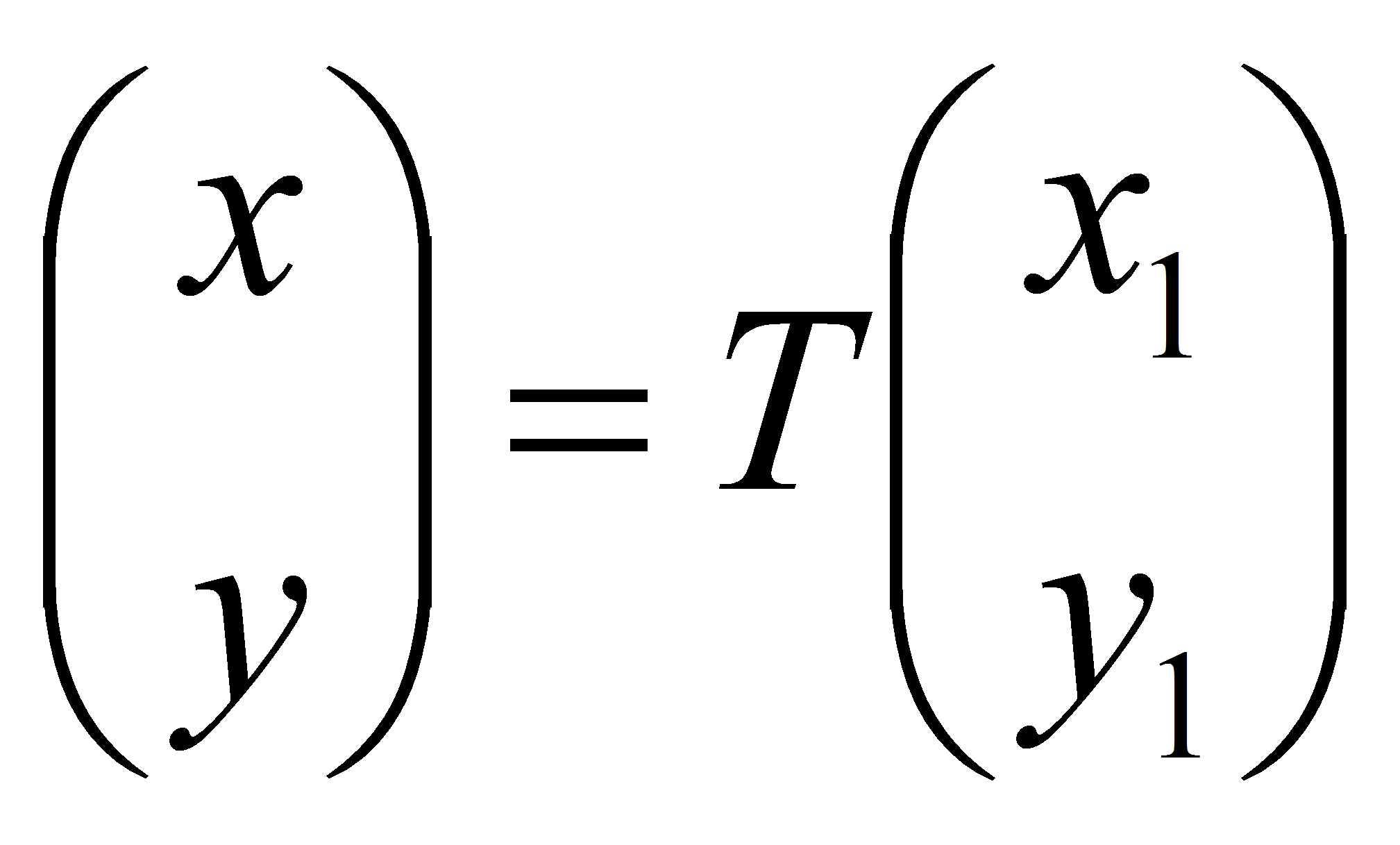В ортонормированном базисе из собственных векторов квадратичная форма имеет канонический вид: , где и - собственные числа матрицы квадратичной формы . При этом формулы преобразования координат имеют вид: , где первый и второй столбец матрицы перехода T являются координатами соответственно первого и второго собственных векторов матрицы А, причем определитель матрицы T>0.