7.Определение собственных чисел и собственных векторов матрицы. Пример отыскания.

Если при умножение квадратной матрицы A на ненулевой вектор получается вектор, || вектору , то говорят что вектор - собственный вектор матрицы A, а - собственное число матрицы А, соответствующее данному собственному вектору.

Пример отыскания:

Дана квадратная матрица второго порядка: . Найти собственные числа и собственные векторы.

Решение:

(1)

Подставим в (1):

=>. Пусть - свободная переменная и =>. Тогда первый собственный вектор будет равен: . Его модуль равен: . Тогда нормированный собственный вектор будет равен: .

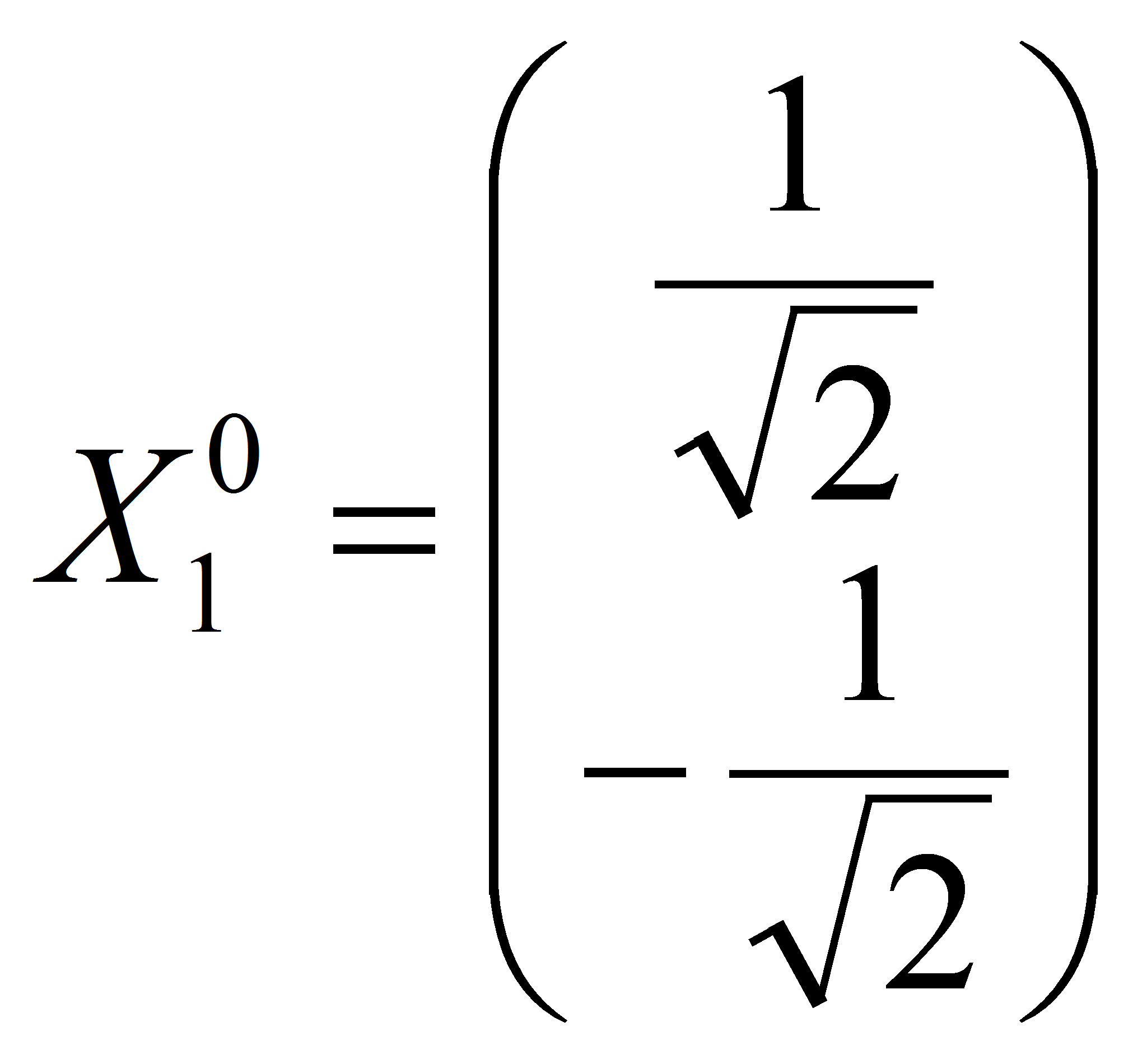Подставим в (1):

=>. Пусть - свободная переменная и =>. Тогда второй собственный вектор будет равен: . Его модуль равен: . Тогда нормированный собственный вектор будет равен: .
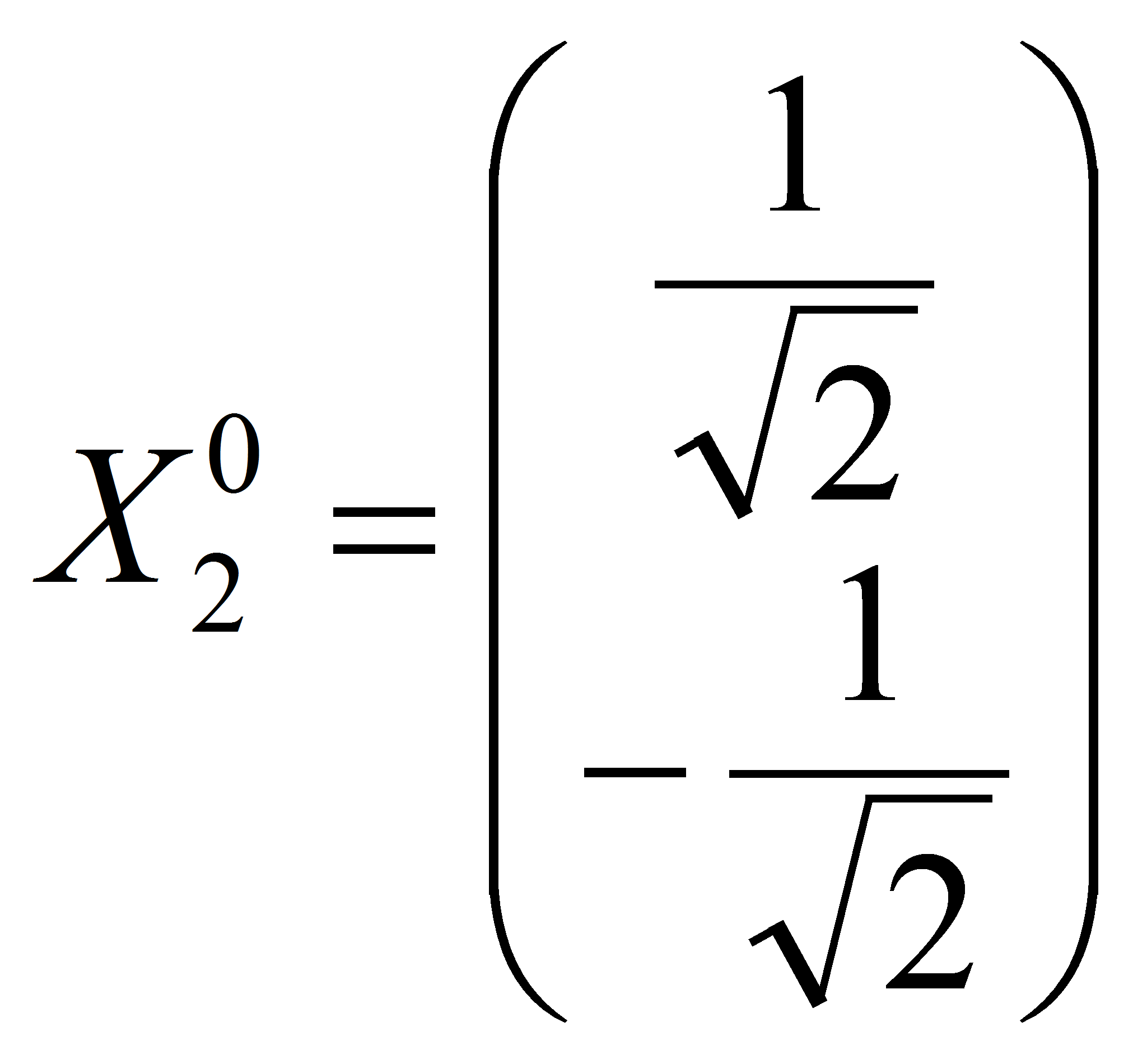