глом
между прямой и плоскостью называется любой из двух смежных углов,
образованных прямой и её проекцией на плоскость:
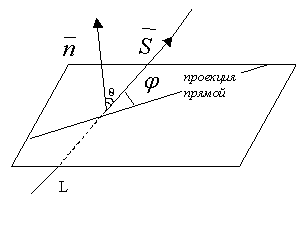
6. Угол между прямой и плоскостью в пространстве. Условия параллельности и перпендикулярности.
Углом
между прямой и плоскостью называется любой из двух смежных углов,
образованных прямой и её проекцией на плоскость:
Обозначим
через
- угол между плоскостью Q
и прямой L,
а через
- угол между векторами
и
.
Тогда
.
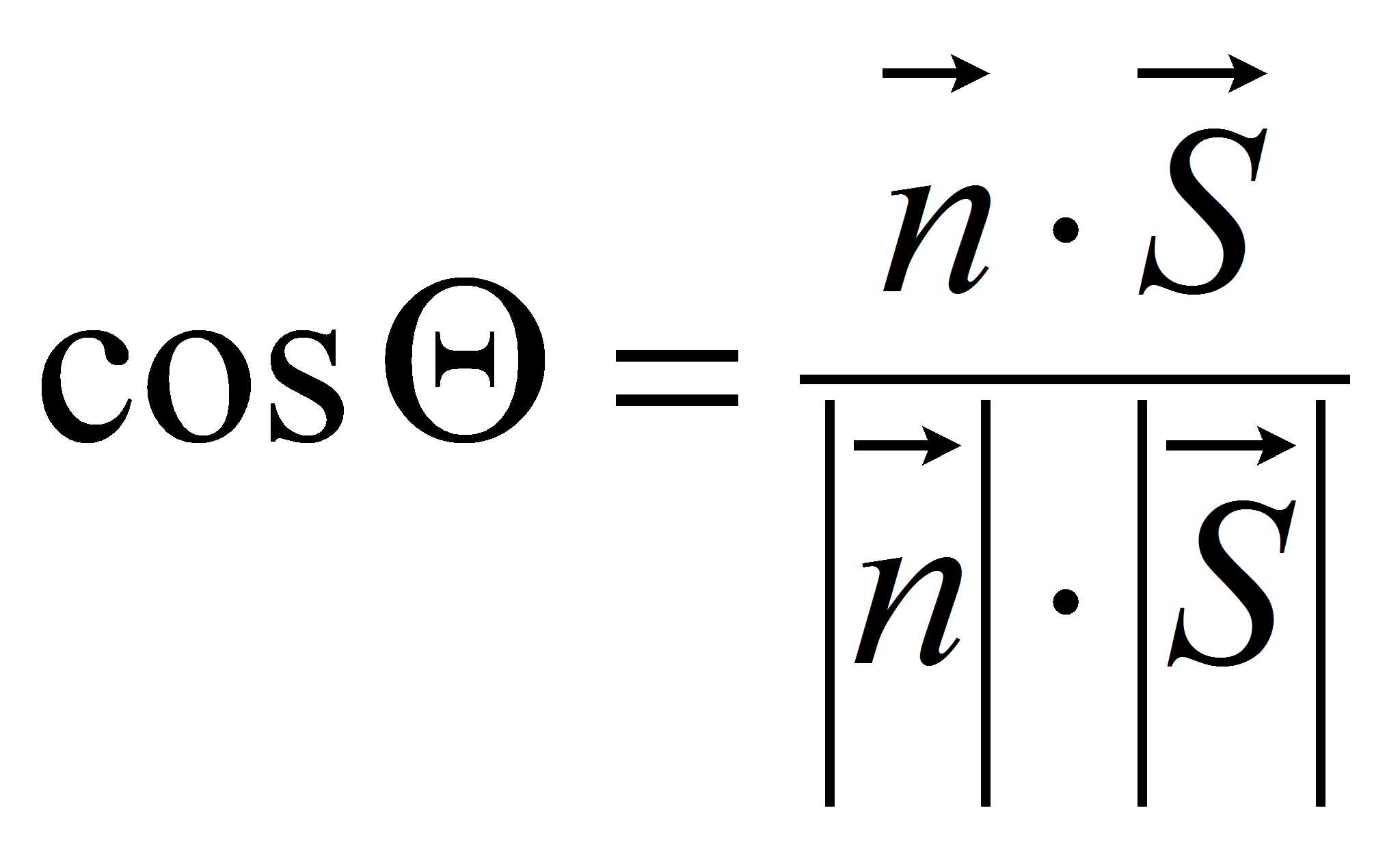Найдем синус угла
:
.
.
|
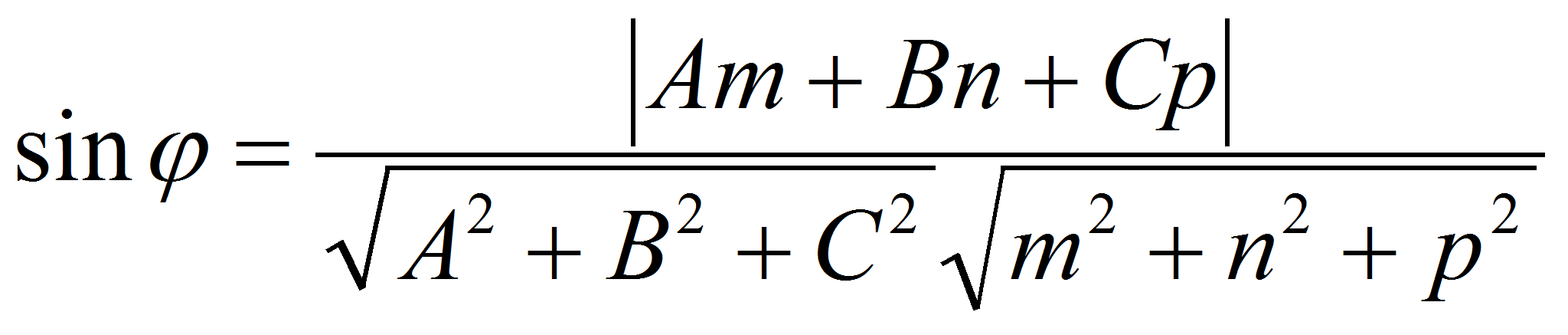Прямая и плоскость
|
Если прямая L
перпендикулярна плоскости Q,
то векторы
|
|
Прямая и плоскость || |
Если прямая L
параллельна плоскости Q,
то векторы
|
и
параллельны, т.е.
.
.