13.Вывод уравнения поверхности вращения. Примеры.

Поверхность вращения - поверхность, образованная вращением некоторой плоской кривой вокруг оси, лежащей в её плоскости.

Вывод уравнения:

Пусть некоторая кривая L, лежит в плоскости Oyz. Уравнения этой кривой запишутся в виде: .

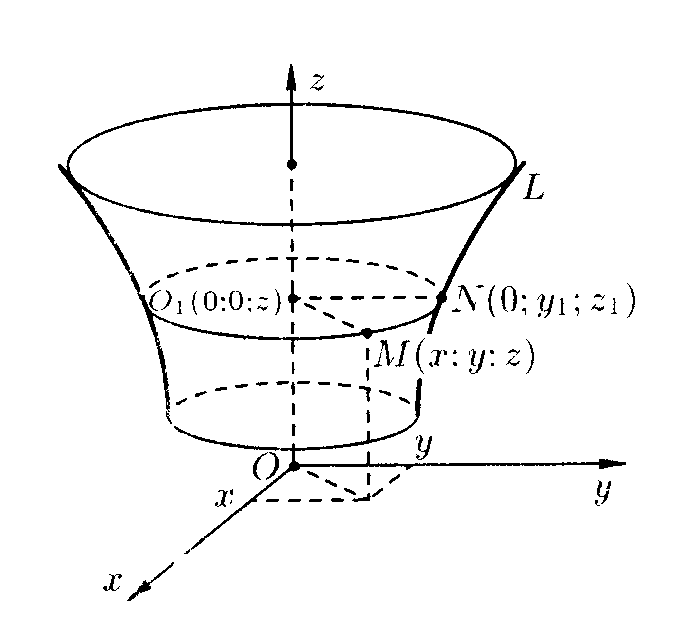
Возьмем на поверхности произвольную точку M(x;y;z). Проведем через точку M плоскость, перпендикулярную оси Oz и кривой L соответственно через O₁ и N. Обозначим координаты точки N через (0;y₁;z₁). Отрезки O₁M и O₁N являются радиусами одной и той же окружности. Поэтому O₁M= O₁N. Но , . Следовательно, , или . Т.к. точка N лежит на кривой L, её координаты y₁ и z₁ удовлетворяют уравнению . Следовательно , => . Это и есть уравнение поверхности вращения.